vuong test package|stata zero inflated negative binomial : dealers vuong: Vuong's non-nested hypothesis test. Description. Compares two models fit to the same data that do not nest via Vuong's non-nested test. Usage. vuong(m1, m2, digits = .
Resultado da Apostadores de Goiânia e Goianésia vão levar R$ 74.293,74 cada. Dezenas sorteadas foram 02-04-24-30-34-50. Há 2 semanas Goiás. Veja mais. Goianésia.
{plog:ftitle_list}
El Hombre Mas Rico De Babilonia
vuong.test(nb1, which.min(nb1$bic), zinb, which.min(zinb$bic)) Compares two models fit to the same data that do not nest via Vuong's non-nested test.We would like to show you a description here but the site won’t allow us.vuong: Vuong's non-nested hypothesis test. Description. Compares two models fit to .
Vuong test Description. Performs Vuong test between two fitted objects of class unitquantreg. Usage vuong.test(object1, object2, alternative = c("two.sided", "less", "greater")) Arguments Description. Compares two models fit to the same data that do not nest via Vuong's non-nested test. Usage. vuong(m1, m2, digits = getOption("digits")) Arguments. .vuong: Vuong's non-nested hypothesis test. Description. Compares two models fit to the same data that do not nest via Vuong's non-nested test. Usage. vuong(m1, m2, digits = .
Vuong test Description. Performs Vuong test between two fitted objects of class unitquantreg. Usage vuong.test(object1, object2, alternative = c("two.sided", "less", "greater")) .The Vuong test is suitable to discriminate between two non-nested models. Usage vuongtest( x, y, type = c("non-nested", "nested", "overlapping"), true_model = FALSE, variance = .
The Vuong (1989) and Clarke (2007) tests are likelihood-ratio-based tests for model selection that use the Kullback-Leibler information criterion. The implemented tests can be used for choosing . plrtest(mod3, mod2, nested=F) # non-nested models. plrtest(mod3, mod1, nested=T) # nested models. Now, from theoretical perspective vuong is a likelihood-ratio . The Vuong test is suitable to discriminate between two non-nested models. Usage vuongtest( x, y, type = c("non-nested", "nested", "overlapping"), true_model = FALSE, .
zinb model formula
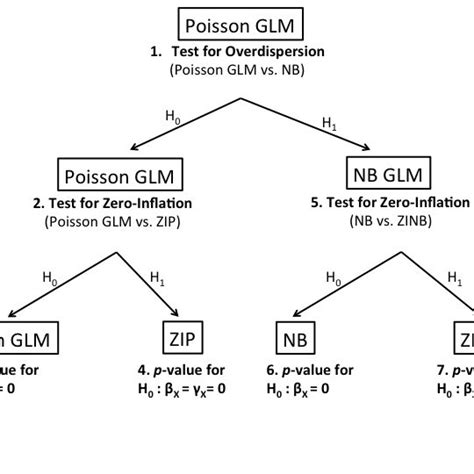
The Vuong test for strictly non-nested models is being widely misused as a test of zero-inflation, even though the original paper of Vuong (1989) does not mention zero-inflation. For example the help page associated with the vuong command in pscl states: “The Vuong non-nested test is based on a comparison of the predicted probabilities of two models that do not .Test pairs of models using Vuong's (1989) theory. This includes a test of model distinguishability and a test of model fit. Rdocumentation. powered by. Learn R Programming. nonnest2 (version 0.5-8) Description Usage . object1, object2: objects of class unitquantreg containing the fitted models.. alternative: indicates the alternative hypothesis and must be one of "two.sided" (default), "less", or "greater".You can specify just the initial letter of the value, but the argument name must be given in .The Vuong non-nested test is based on a comparison of the predicted probabilities of two models that do not nest. Examples include comparisons of zero-inflated count models with their non-zero-inflated analogs (e.g., zero-inflated Poisson versus ordinary Poisson, or zero-inflated negative-binomial versus ordinary negative-binomial).
Vuong's test for non-nested models Description. Since it is possible to fit power law models to any data set, it is recommended that alternative distributions are considered. A standard technique is to use Vuong's test. This is a likelihood ratio test for model selection using the Kullback-Leibler criteria.Optional analysis: Vuong test to compare Poisson, negative binomial, and zero-inflated models . The Vuong test, implemented by the pscl package, can test two non-nested models. It works with negbin, zeroinfl, and some glm model objects which are fitted to the same data.
x: a first fitted model of class "mhurdle",. y: a second fitted model of class "mhurdle",. type: the kind of test to be computed, true_model: a boolean, TRUE if one of the models is asumed to be the true model, variance: the variance is estimated .
The Vuong test is suitable to discriminate between two non-nested models.Like AIC and BIC, the Vuong test statistic may be corrected for the number of parameters used in the models. There are two possible corrections; the Akaike and the Schwarz corrections, which correspond to the penalty terms in the AIC and the BIC, respectively. . You should contact the package authors for that. Tweet to @rdrrHQ GitHub issue . Therefore, when comparing these two models, AIC or BIC are used, and Vuong's test in R is irrelevant (to my understanding) as it says it should be used in non-nested models, example ordinary Poisson vs zero-ordinary Poisson model. On the other hand, I would like to compare two models. In the first one one of the variables are taken as continuous.
The Vuong test [21] is not used on . Here, we developed a Python-based package (TensorZINB) to solve the zero-inflated negative binomial (ZINB) model using the TensorFlow deep learning framework .In the Vuong test, the null hypothesis is that the two models are equally close to the actual model, whereas the alternative is that one model is closer. The test follows asymptotically a standard normal distribution under the null. Assume that the critical region is (-c,c), where c is typically set to 1.96.
Vuong Test Comparing Two R-Vine Copula Models Description. This function performs a Vuong test between two d-dimensional R-vine copula models as specified by their RVineMatrix() objects. Usage RVineVuongTest(data, RVM1, RVM2) Arguments Well, from technical perspective, vuong function accepts regression model objects from classes glm, negbin or zeroinfl. As coxph is an object of different class, you probably can´t feed it to vuong function. You can feed the coxph to plrtest which is partial likelihood ratio test for non-nested coxph models:
zinb
Vuong's Test - test_vuong(): Vuong's (1989) test can be used both for nested and non-nested models, and actually consists of two tests. The Test of Distinguishability (the Omega2 column and its associated p-value) indicates whether or not the models can possibly be distinguished on the basis of the observed data. If its p-value is significant .If you do not have a package installed, run: install.packages("packagename"), or if you see the version is out of date, run: update.packages(). . In times past, the Vuong test had been used to test whether a zero-inflated negative binomial .364 The Misuse of The Vuong Test 2 The Misuse of the Vuong Test The Vuong test for strictly non-nested models is being widely misused as a test of zero-in ation. For example the help page associated with the vuong command in pscl states: \The Vuong non-nested test is based on a com-parison of the predicted probabilities of two models that do . Vuongtest: Vuong's test for non-nested model comparison In spatcounts: Spatial count regression. . Note that we can't provide technical support on individual packages. You should contact the package authors for that. Tweet to @rdrrHQ GitHub issue tracker [email protected] Personal blog .
FactorCopula-package: Factor, bi-factor, second-order and factor tree copula models; GSS: The 1994 General Social Survey; . We compute the Vuong's test between the factor copula model with BVN copulas (that is the standard factor model) and a competing factor copula model to reveal if the latter provides better fit than the standard factor model.Vuong (1989)'s test for the comparison of non-nested copula mixed models for diagnostic test accuaracy studies. It shows if a copula mixed model provides better fit than the standard GLMM. We compute the Vuong's test with Model 1 being the copula mixed model with BVN copula and normal margins, i.e., the standard GLMM.'Vuongtest' suggests the better of two (not necessarily nested) models according to Vuong's statistic for the parameters in each of the iterations. Rdocumentation. powered by. Learn R Programming. spatcounts (version 1.1) Description Usage. Arguments. References. See Also. Examples Run this code .
The Vuong test for model selection is a statistical method used to compare the predictive power of two competing models, particularly in cases where the models are non-nested. This test calculates a test statistic based on the likelihood functions of both models to determine which one fits the data better. It is especially useful in contexts like count data models, where traditional . The two-sided test indicates that the two models have (statistically) significantly different fit for the observed data when it rejects , and the one-sided test indicates that model fits the observed data significantly better when it rejects .It is the goal of this paper to develop a simple test of equal fitting with uniform asymptotic validity and good power properties. CDVine-package: Statistical inference of C- and D-vine copulas; CDVinePar2Tau: Kendall's tau values of a vine copula model; . Like AIC and BIC, the Vuong test statistic may be corrected for the number of parameters used in the models. There are two possible corrections; the Akaike and the Schwarz corrections, which correspond to the penalty . the size of the test. pval: should the p-value be computed ? nested: a boolean, TRUE for nested models. vartest: a boolean, if TRUE, the variance test is computed. ndraws: the number of draws for the simulations. diffnorm: a creuser. seed: the seed. numbers: a user provided matrix of random numbers. nd: a boolean, if TRUE (the default) the non .
I performed the following Vuong test for panel data with fixed effects as suggested by Prof. Wooldridge (reasoned from Section 13.11.2 in 2010 MIT Press book, Econometric Analysis of Cross Section and Panel Data) in the following URL. Details. Let us denote by { \ell}^{(1)},\,{\bm \ell}^{(2)} the vectors of pointwise loglikelihoods for a model with copula family 1 and 2 respectively. Here, we assume that both models have the same degrees of freedom, i.e. the same number of parameters. We now compute the differences of the pointwise loglikelihood as
falling ball impact test
falling ball impact test standard
webWe would like to show you a description here but the site won’t allow us.
vuong test package|stata zero inflated negative binomial